다이나믹 프로그래밍_11054 : 가장 긴 바이토닉 부분 수열 JAVA
문제
수열 S가 어떤 수 Sk를 기준으로 S1 < S2 < ... Sk-1 < Sk > Sk+1 > ... SN-1 > SN을 만족한다면, 그 수열을 바이토닉 수열이라고 한다.
예를 들어, {10, 20, 30, 25, 20}과 {10, 20, 30, 40}, {50, 40, 25, 10} 은 바이토닉 수열이지만, {1, 2, 3, 2, 1, 2, 3, 2, 1}과 {10, 20, 30, 40, 20, 30} 은 바이토닉 수열이 아니다.
수열 A가 주어졌을 때, 그 수열의 부분 수열 중 바이토닉 수열이면서 가장 긴 수열의 길이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 수열 A의 크기 N이 주어지고, 둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ N ≤ 1,000, 1 ≤ Ai ≤ 1,000)
출력
첫째 줄에 수열 A의 부분 수열 중에서 가장 긴 바이토닉 수열의 길이를 출력한다.
예제 입력 1 복사
10
1 5 2 1 4 3 4 5 2 1
예제 출력 1 복사
7
접근방법
- 바이토닉이란 특정한 값을 기준으로 왼쪽 부분은 오름차순, 오른쪽 부분은 내림차순인 수열 또는 그러한 부분 순환이동을 말합니다.
- 왼쪽에서 오른쪽으로 가는 오름차순 길이를 나타내는 배열을 정합니다.

r_dp[0] = {1} : 길이 1
r_dp[1] = {1, 5} : 길이 2
r_dp[2] = {1, 2} : 길이 2
r_dp[3] = {1} : 길이 1
r_dp[4] = {1, 2, 4} : 길이 3
r_dp[5] = {1, 2, 3} : 길이 3
r_dp[6] = {1, 2, 3, 4} : 길이 4
r_dp[7] = {1, 2, 3, 4, 5} : 길이 5
r_dp[8] = {1, 2} : 길이 2
r_dp[9] = {1} : 길이 1
- 오른쪽에서 왼쪽으로 가는 내림차순 수열의 길이를 나타내는 배열을 정합니다.

[역방향]
l_dp[9] = {1} : 길이 1
l_dp[8] = {1, 2} : 길이 2
l_dp[7] = {1, 2, 5} : 길이 3
l_dp[6] = {1, 2, 4} : 길이 3
l_dp[5] = {1, 2, 3} : 길이 3
l_dp[4] = {1, 2, 3, 4} : 길이 4
l_dp[3] = {1} : 길이 1
l_dp[2] = {1, 2} : 길이 2
l_dp[1] = {1, 2, 3, 4, 5} : 길이 5
l_dp[0] = {1} : 길이 1
- 오름차순 배열과 내림차순 배열을 합칩니다.
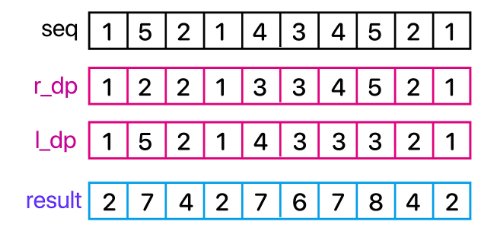
- 원소가 1개씩 중복되어 있으므로, 결과값에서 1씩 빼줍니다.

result[0] = (r_dp[0] + l_dp[0]) = {1} + {1} = {1} : 길이 1
result[1] = (r_dp[1] + l_dp[1]) = {1, 5} + {5, 4, 3, 2, 1} = {1, 5, 4, 3, 2, 1} : 길이 6
result[2] = (r_dp[2] + l_dp[2]) = {1, 2} + {2, 1} = {1, 2, 1} : 길이 3
result[3] = (r_dp[3] + l_dp[3]) = {1} + {1} = {1} : 길이 1
result[4] = (r_dp[4] + l_dp[4]) = {1, 2, 4} + {4, 3, 2, 1} = {1, 2, 4, 3, 2, 1} : 길이 6
result[5] = (r_dp[5] + l_dp[5]) = {1, 2, 3} + {3, 2, 1} = {1, 2, 3, 2, 1} : 길이 5
result[6] = (r_dp[6] + l_dp[6]) = {1, 2, 3, 4} + {4, 2, 1} = {1, 2, 3, 4, 2, 1} : 길이 6
result[7] = (r_dp[7] + l_dp[7]) = {1, 2, 3, 4, 5} + {5, 2, 1} = {1, 2, 3, 4, 5, 2, 1} : 길이 7
result[8] = (r_dp[8] + l_dp[8]) = {1, 2} + {2, 1} = {1, 2, 1} : 길이 3
result[9] = (r_dp[9] + l_dp[9]) = {1} + {1} = {1} : 길이 1
다이내믹 프로그래밍 Buttom-up 방식을 이용하고 입력값은 BufferedReader를 사용하였다.
import java.io.*;
import java.util.*;
class Main{
static int N;
static int[] arr;
static int[] r_dp;
static int[] l_dp;
public static void main(String[] args){
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
arr = new int[N];
r_dp = new int[N];
l_dp = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine()," ");
for(int i=0;i<N;i++){
arr[i] = Integer.parseInt(st.nextToken());
}
LIS();
LDS();
int max = 0;
for(int i=0;i<N;i++){
if(max<r_dp[i]+l_dp[i]){
max = r_dp[i]+l_dp[i]
}
System.out.println(max-1);
}
}
public static void LIS(){
for(int i=0;i<N;i++){
r_dp[i] = 1;
for(int j=0;j<i;j++){
if(arr[i]>arr[j]&&r_dp[i]<r_dp[j]+1){ // i번째 원소가 j번째보다 크면서, j번째 dp값에서 1더한 값이 i번째 dp 원소보다 크다면
r_dp[i] = r_dp[j] + 1; // i번째 dp값은 j번째 dp값+1이 된다.
}
}
}
}
public static void LDS(){
for(int i=N-1;i>=0;i--){
l_dp[i] = 1;
for(int j=N-1;j>i;j--){
if(arr[i]>arr[j]&&l_dp[i]<l_dp[j]+1){
l_dp[i] = l_dp[j] + 1;
}
}
}
}
}