문제
3×N 크기의 벽을 2×1, 1×2 크기의 타일로 채우는 경우의 수를 구해보자.
입력
첫째 줄에 N(1 ≤ N ≤ 30)이 주어진다.
출력
첫째 줄에 경우의 수를 출력한다.
예제 입력 1 복사
2
예제 출력 1 복사
3
힌트
아래 그림은 3×12 벽을 타일로 채운 예시이다.

풀이과정
1. 1*2 이나 2*1 타일로 해야되기 때문에 무슨 짓을 하던 n이 홀수라면 전체 칸 수(3*n)이 홀수 이므로 2칸짜리 타일로 타일링이 불가합니다. 즉 n이 짝수일때만 타일링이 가능합니다. 이 부분은 예외로 처리합니다.
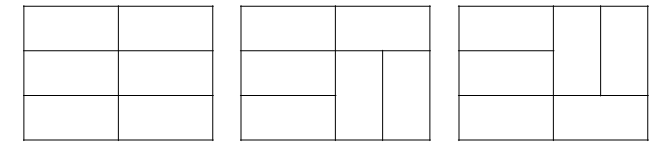
2. n=2일때 3가지 모양이 나옵니다.

3. n=4일때 n=2일때 나왔던 모양에서 3가지 모양이 더 추가되므로, (n=2에서 나온 모양수) * (3) 임을 알 수 있습니다.
그럼 f(4) = f(2)*3 임을 알 수 있습니다.
4. 다음으로 n=4일때 예외로 추가되는 규칙이 있습니다. 2개로 나눴을 때 중간에 겹치는 부분을 활용한 다음의 타일링이 있습니다.

그럼 일단 최종적으로 n=4일때 f(4) = f(2)*3+2 = 11 임을 알 수 있습니다.
5. n = 6일때 일단 f(4) * 3 은 확실합니다.거기에 예외로 추가되는 2개까지 포함하여 f(6) = f(4)*3 + 2까지 생각할 수 있습니다.

6. n=2일때는 예외가 0, n=4일때부터 예외가 항상 2개 였습니다. 그렇다면 n=6일때 예외 2개를 활용할 수 있고, n=4일때 예외를 활용하여 n=8을 만들 수 있습니다.
그래서 f(8) = f(6) *3 + 2 + f(2)*2{n=6 예외갯수} + f(4) *2{n=4 예외갯수} 임을 알 수 있습니다.
그렇게 해서 나오게 되는 코드는 다음과 같습니다.
import java.io.*;
class Main{
public static void main(String[] args){
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
if(N%2!=0){
System.out.println(0);
return;
}
int[] dp = new int[Math.max(N/2,2)];
dp[0] = 3;
dp[1] = 11;
int tmp = 0;
for(int i=2;i<n/2;i++){
dp[i] = dp[i-1]*3+2(tmp+=dp[i-2]*2);
}
System.out.println(dp[N/2-1]);
}
}'알고리즘 기초1 Java' 카테고리의 다른 글
| 다이나믹 프로그래밍_1912 : 연속합 JAVA (0) | 2024.05.02 |
|---|---|
| 다이나믹 프로그래밍_11054 : 가장 긴 바이토닉 부분 수열 JAVA (0) | 2024.04.29 |
| 다이나믹 프로그래밍_10844 : 가장 긴 감소하는 부분 수열 JAVA (0) | 2024.04.22 |
| 다이나믹 프로그래밍_10844 : 가장 긴 증가하는 부분 수열 JAVA (0) | 2024.04.13 |
| 다이나믹 프로그래밍_2193 : 이친수 JAVA (0) | 2024.04.06 |



